二阶常系数线性非齐次微分方程的通解和特解
有二阶常系数线性非齐次微分方程
1. 如果 g(t) 里有指数函数,在特解里也要用相同的指数函数。
例:
先把方程设齐次:
然后解通解:
通解:
然后解特解:
带入原方程:
特解:
最后:
2. 如果 g(t) 是多项式,在特解里要用通用相同次数的多项式。
例:
通解:
然后解特解:
代入原方程:
化简,比较系数得:
特解:
最后:
3. 如果 g(t) 里含有cos或者sin函数,特解里要用cos和sin函数。
例:
通解:
然后解特解:
代入原方程:
化简,比较系数得:
特解:
最后:
4. 如果 g(t) 是n个函数相加,那么要把方程拆分成n个部分,依次求特解。
得:
对以上的n个微分方程依次求特解。
例:
通解:
然后解特解:
特解:
最后:
5. 列出预选的特解,一定要和通解进行比较。如果预选特解中和通解中出现重复项,那么要在特解上乘以t,直到不再出现重复项。
例:
通解:
由于
因此初选特解
但是 y~p~ 和 y~c~ 中第一项相同,那么要在 y~p~ 乘以 t ,得,
但是 y~p~ 和 y~c~ 中第二项也相同,那么再乘以 t ,得,
把特解和通解再比较,没有重复了。特解选好了。
代入原方程得:
特解:
最后:
6. 如果 g(t) 是两个或两个以上函数相乘,那么特解中要用 g(t) 中每个函数对应的特解相乘来求解。
例:
通解:
g(t)是由几个函数相乘再相加所得,先要把它拆分开来。是由二次多项式和sin函数相乘所得。特解中要用通用二次多项式、cos和sin函数。
设特解和通解
比较,发现 Ccos(3t) 和 Fsin(3t) 和通解有相同项。那么,要在 y~p1~基础上乘以 t ,
得:
即
再比较,没有相同项了。然后,是由指数函数和cosine函数相乘所得。特解中要用指数函数、cos和sin函数。设特解
然后和通解 y~c~ 比较,没有相同项。
最后:
总结:
- 如果 g(t) 中出现指数函数 (e^at^),在特解里也要用相同的指数函数。
- 如果 g(t) 是多项式,在特解里要用通用相同次数的多项式。
- 如果 g(t) 里出现任意一个cos或者sin函数,特解里要用cos和sin函数。
- 如果 g(t) 是n个函数相加,
,那么要把方程拆分成n个部分,依次求特解。
- 列出预选的特解,一定要和通解先进行比较。如果预选特解中和通解中出现重复项,那么要在特解上乘以 t ,直到不再出现重复项。
- 如果 g(t) 是两个或两个以上函数相乘,那么特解中要用 g(t) 中每个函数对应的特解相乘来求解。
二阶常系数线性非齐次微分方程的通解和特解
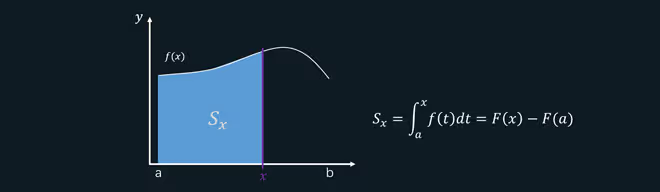
1.变上限积分和原函数关系
2.泰勒公式通俗理解
3.曲线曲率公式的推导
4.均值不等式的几何意义
5.数列求和-自然数平方和
6.格林公式挖洞法中内曲线顺时针的直观解释
7.反常积分敛散性判定
8.不定积分常用公式
1.absolute和relative定位
2.display:table-cell在布局上的应用
3.两列布局css
4.解决GitHub访问不了问题
5.Collection集合和Map集合
6.JDK,JRE和JVM