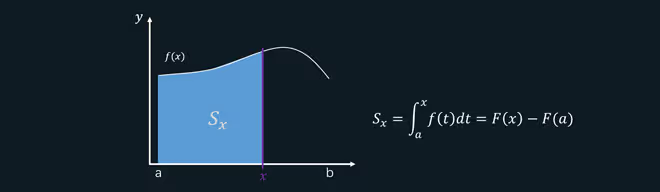
变上限积分和原函数关系

本文将会带你透彻搞懂以下三个东西（以变上限积分函数为例）：

1.变上限积分与原函数有什么关系？
2.分段函数的变上限积分如何求？
3.变上限积分在被积函数第一类间断点处如何（连续or可导？）

Q1：变上限积分与原函数的关系？

要弄清楚它们之间的关系，首先我们来看定积分和不定积分是什么。

1.什么是不定积分？

说白了，不定积分就是求被积函数的一系列原函数（考虑到后面加了个任意常数c）。

所以一个函数有不定积分就可以说它有原函数。

2.什么是定积分？

定积分最初被发明出来是为了求不规则图形的面积，它是与面积有关的。

所以如果能求出一个函数在某个区间与x轴围成的面积，那么它在这个区间的定积分就是存在的，也可以说这个函数在这个区间是可积的。

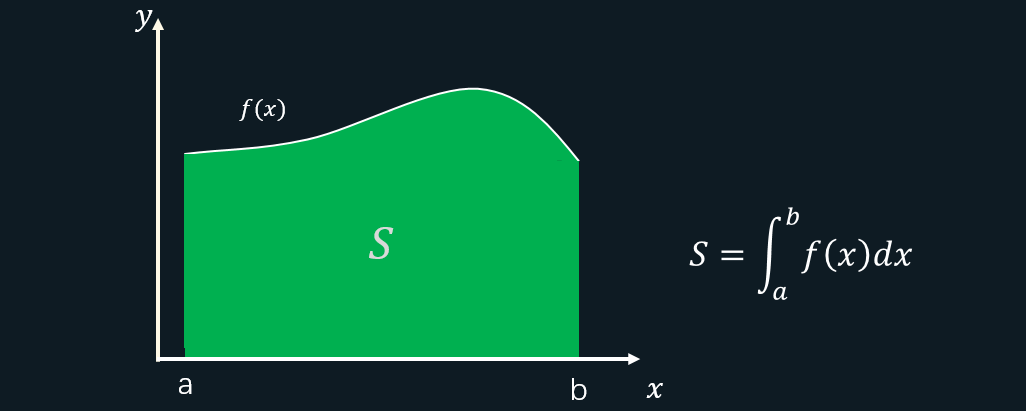
3.定积分和原函数的关系：

那么他们之间有什么关系呢？其实一开始他们之间一点关系都没有。直到后来一个“牛掰”的理论将它们建立了联系，它就是牛顿-莱布尼兹。它是这样说的：

一个连续函数在区间[a,b] 上的定积分等于它的任意一个原函数在区间 [a,b] 上的增量 注：连续这两个字很关键

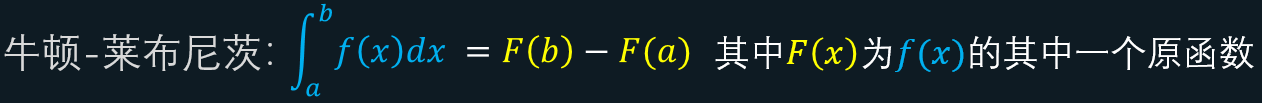
这样就将原函数与定积分联系在了一起。

a. f(x)连续时，变上限积分和原函数的联系：

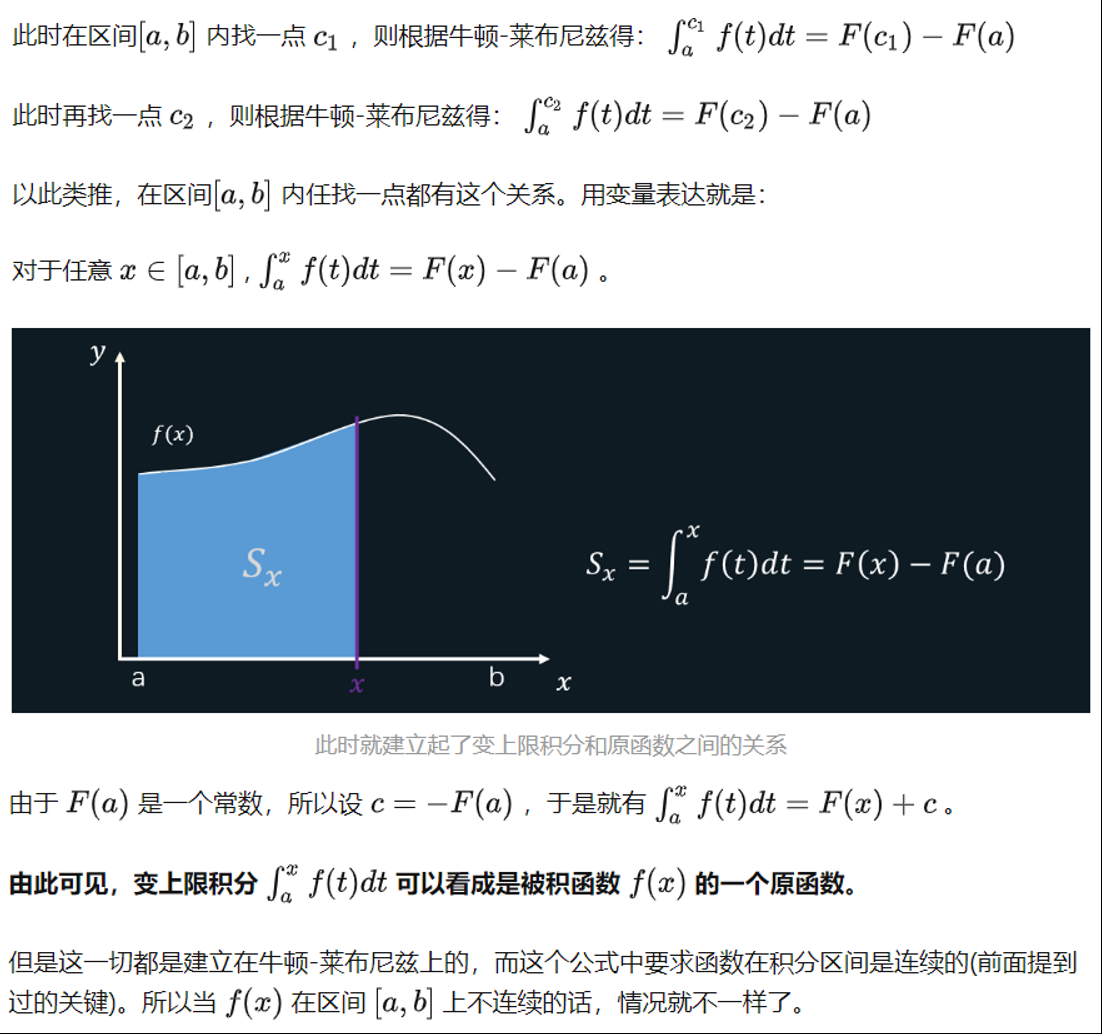
b. f(x) 不连续时，两者的情况：

首先看原函数：

p.s.接下来会有小伙伴问：

再看变限积分：

Q2：分段函数的变上限积分如何求？

考研常常研究的是有界分段函数的变上限积分，且函数在每个分段区间内是连续的。因此我们主要研究分段点处的情况，一般来说分为以下三种情况：

1.分段点处连续；2.分段点为可去间断点；3.分段点为跳跃间断点

以下针对这三种情况来研究：

1.分段点处连续

此时分段函数在定义域内是连续的，所以可以用牛顿-莱布尼茨进行计算：

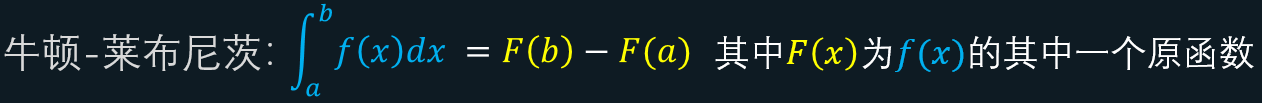
那么此时原函数怎么算呢？具体如下：

2.分段点为可去间断点

根据之前所讲，有若干个可去间断的函数所围成的面积等于对应连续函数所围成的面积。所以我们直接算连续函数围成的面积就可以，而连续函数所围成的面积可以通过牛顿-莱布尼茨算，这样就搞定了。

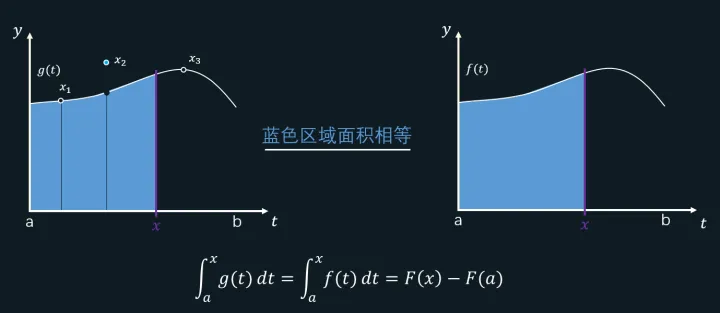
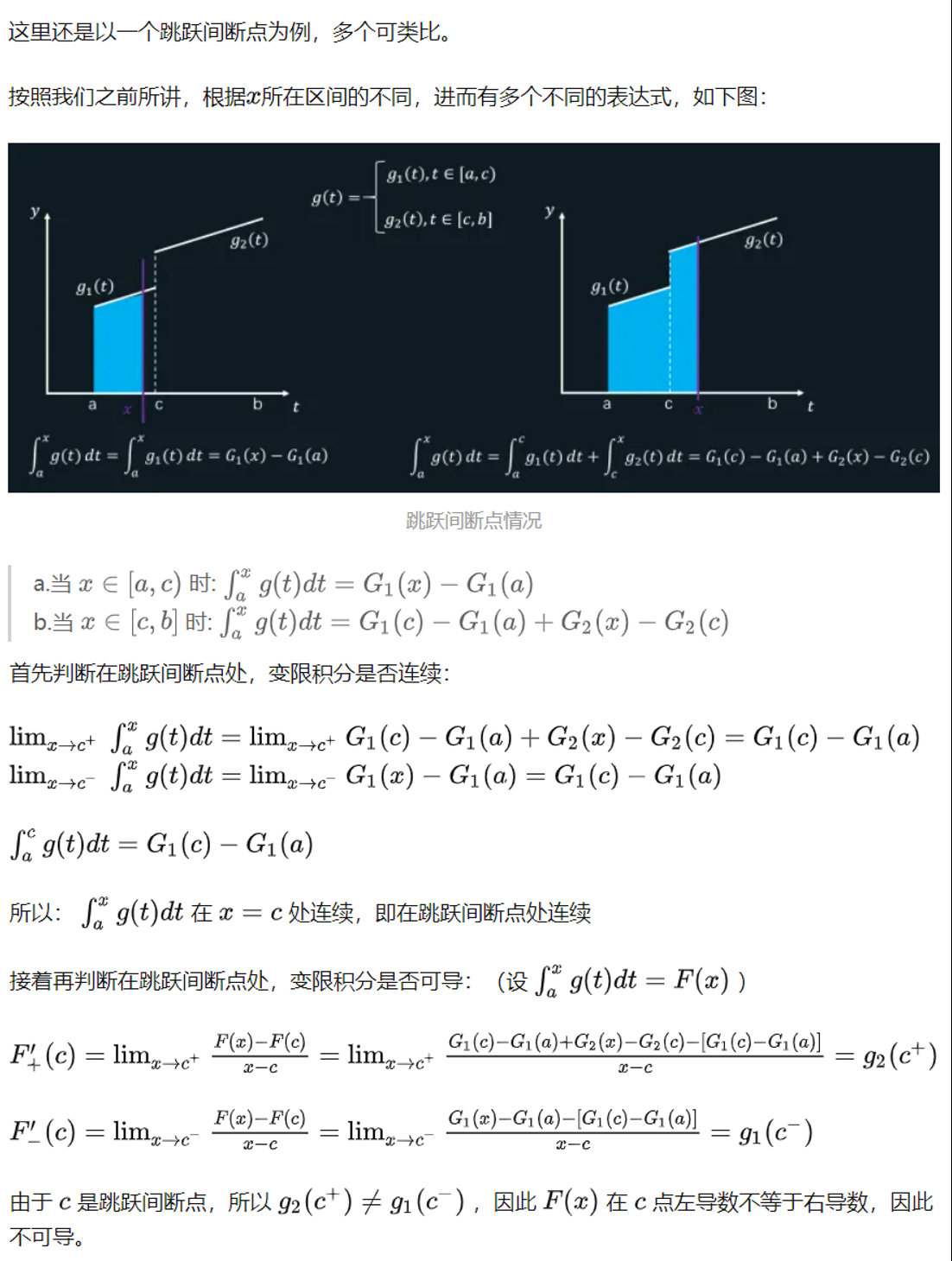
3.分段点为跳跃间断点

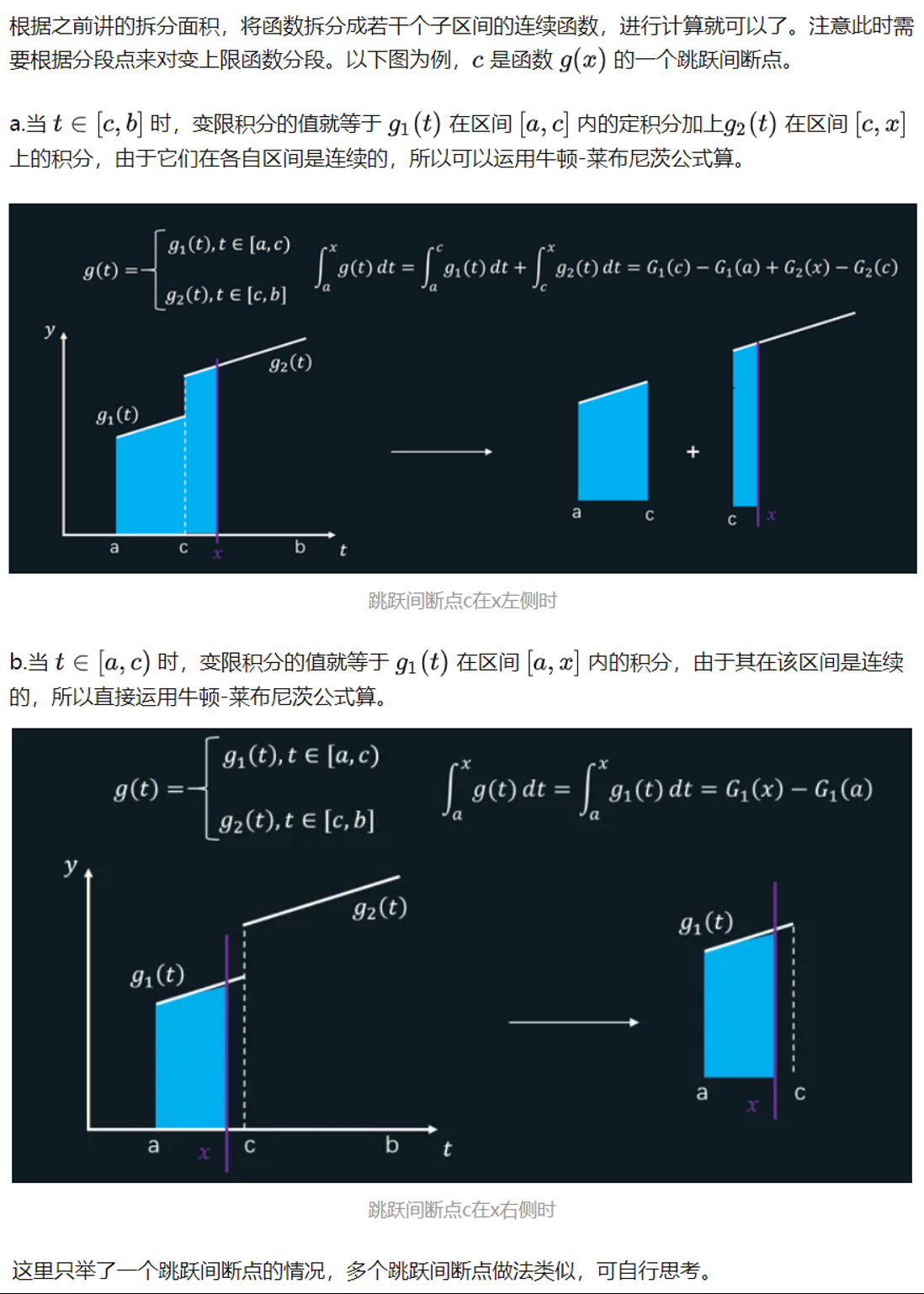
重点技巧：观察三种情况，对于求分段函数的变上限积分函数，有一个通用做法：

Q3：变上限积分在被积函数第一类间断点处如何（连续or可导）？

还是分别以可去间断点和跳跃间断点来说明：

1.可去间断点

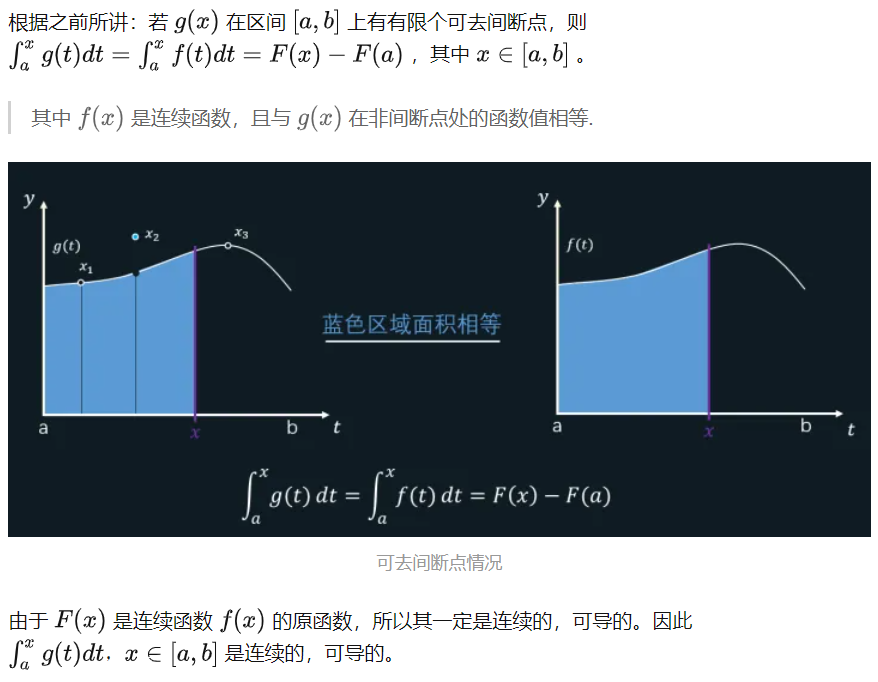
2.跳跃间断点

三个问题结束，针对上述三个问题的总结如下：