大顶堆的构建和排序

堆的定义

堆是一种非线性结构，可以把堆看作一棵二叉树，也可以看作一个数组，即：堆就是利用完全二叉树的结构来维护的一维数组。

堆可以分为大顶堆和小顶堆。
大顶堆：每个结点的值都大于或等于其左右孩子结点的值。
小顶堆：每个结点的值都小于或等于其左右孩子结点的值。

如果是排序，求升序用大顶堆，求降序用小顶堆。

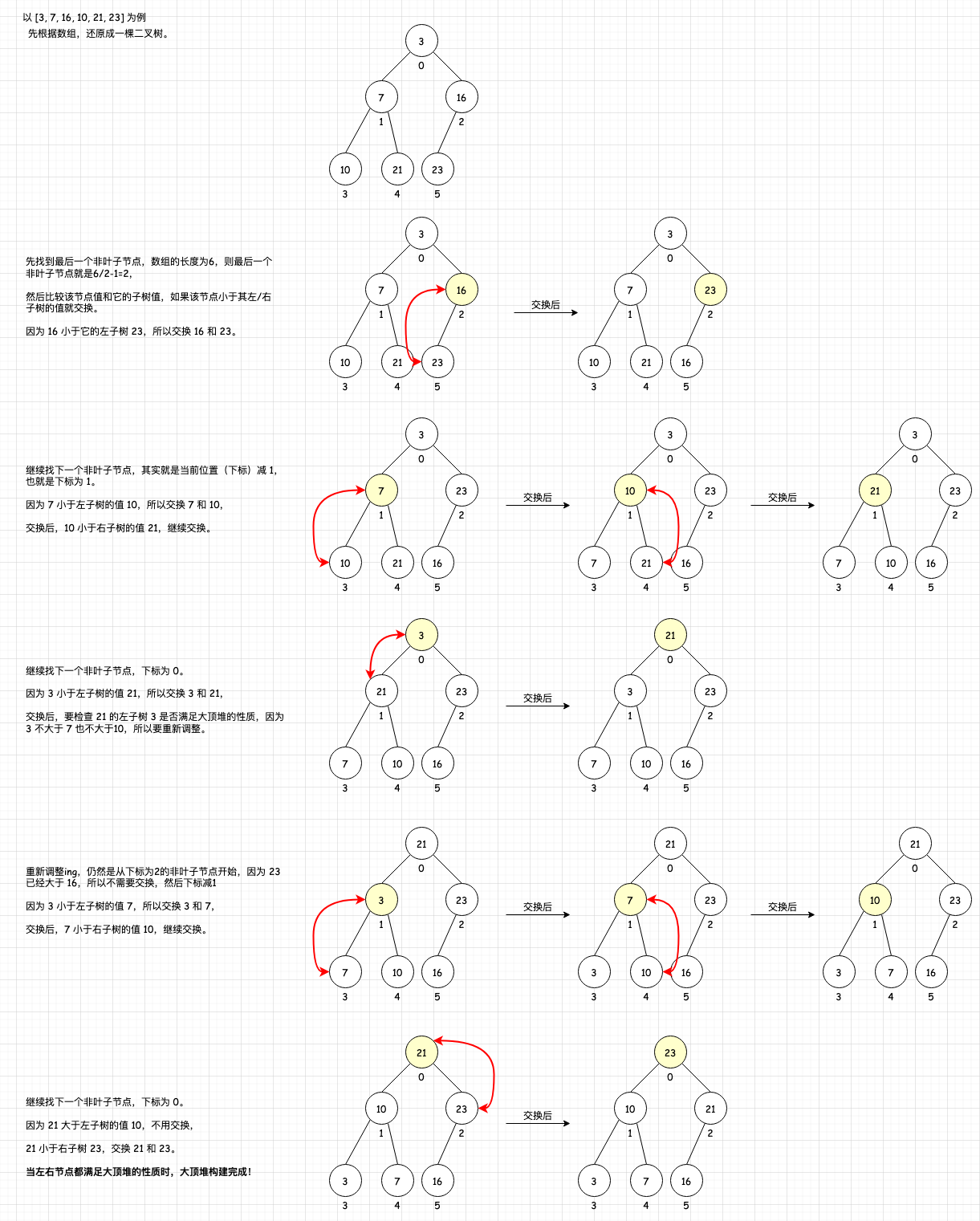
大顶堆的构建过程

从最底层的非叶结点开始，调整完该层以后再往上调整；

比较当前结点的值和左子树的值，如果当前节点小于左子树的值，就交换当前结点和左子树；
交换完后要检查左子树是否满足大顶堆的性质，不满足则重新调整子树结构；

再比较当前结点的值和右子树的值，如果当前结点小于右子树的值，就交换当前结点和右子树；
交换完后要检查右子树是否满足大顶堆的性质，不满足则重新调整子树结构；

无需交换调整的时候，则大顶堆构建完成。

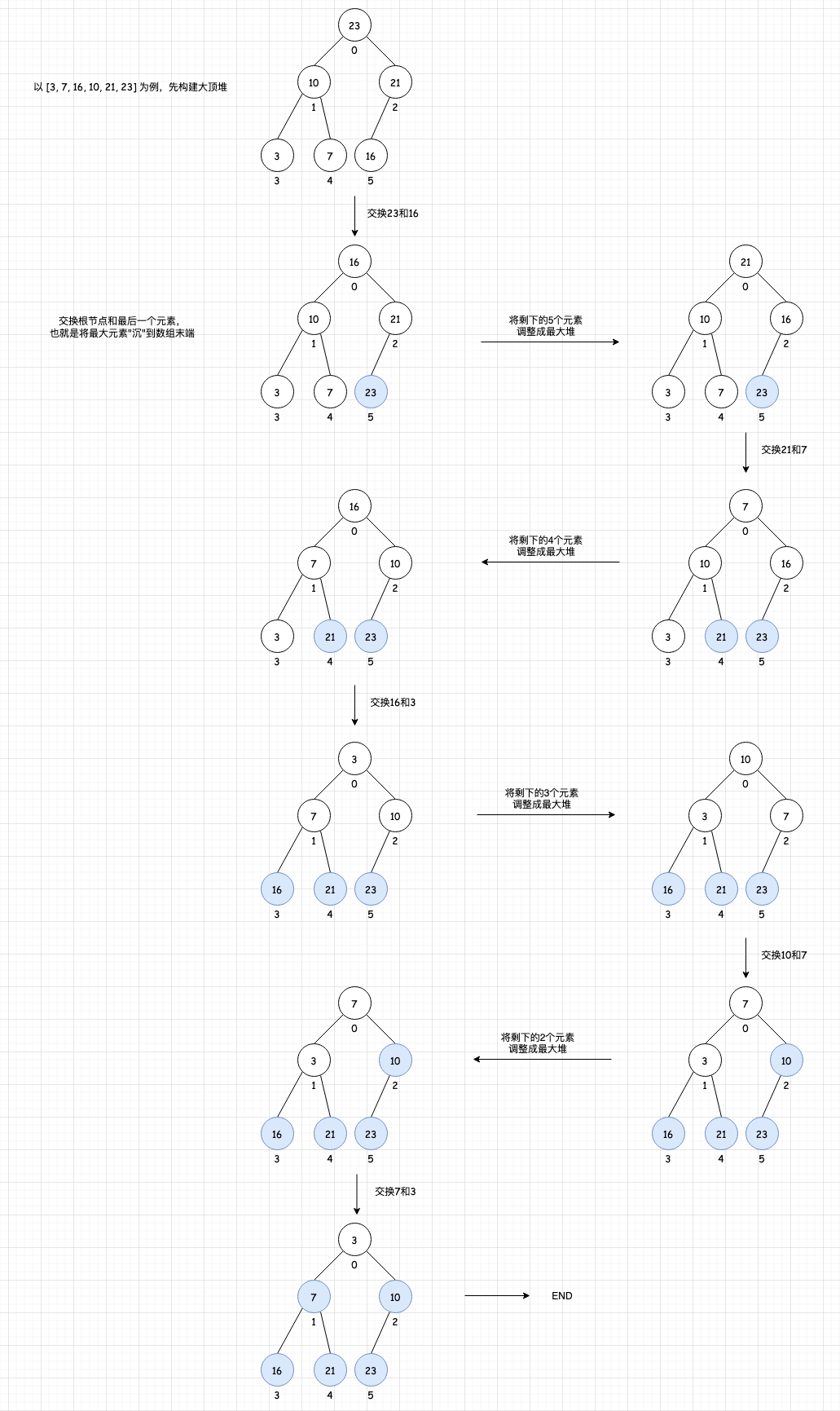
大顶堆的排序过程

先 n 个元素的无序序列，构建成大顶堆；

将根结点与最后一个元素交换位置；

交换过后将剩下的 n-1 个元素重新构建成大顶堆。

一直到根结点的时候，则大顶堆构建完成。